|
The Natural Element Method in Solid Mechanics
N. Sukumar
Ph.D. Thesis
Theoretical and Applied Mechanics
Northwestern University
Please refer to the Ph.D. thesis web page for
details.
The Natural Element Method in Solid Mechanics
N. Sukumar, B. Moran and T. Belytschko
International Journal for Numerical Methods in Engineering
Vol. 43, Number 5, pp. 839-887, 1998
Abstract
The application of the Natural Element Method (NEM)
(Traversoni (1994),
Braun and Sambridge (1995))
to boundary value problems in two-dimensional
small displacement elastostatics is
presented. The discrete model of the
domain
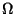 consists
of a set of distinct nodes N, and
a polygonal description of the boundary consists
of a set of distinct nodes N, and
a polygonal description of the boundary
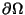 . In
the natural element method, the trial and test functions are
constructed using natural neighbor interpolants. These interpolants
are based on the Voronoi tessellation of the set of nodes
N. The interpolants are smooth
( . In
the natural element method, the trial and test functions are
constructed using natural neighbor interpolants. These interpolants
are based on the Voronoi tessellation of the set of nodes
N. The interpolants are smooth
(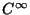 )
everywhere, except at the nodes where they are
C0. In
one-dimension, NEM is identical to linear finite elements. The
NEM interpolant is strictly linear between adjacent nodes on the
boundary of the convex hull, which
facilitates imposition of essential boundary conditions. A
methodology to model material
discontinuities and non-convex bodies (cracks) using
NEM is also described. A standard
displacement-based Galerkin procedure is used to obtain the
discrete system of linear equations. Application
of NEM to various problems in solid mechanics, which include,
the patch test, gradient problems, bimaterial interface,
and a static crack problem are presented. Excellent agreement with
exact (analytical) solutions is obtained, which exemplifies the
accuracy and robustness of NEM and suggests its potential
application in the context of other classes of problems--crack
growth, plates, and large deformations to name a few. )
everywhere, except at the nodes where they are
C0. In
one-dimension, NEM is identical to linear finite elements. The
NEM interpolant is strictly linear between adjacent nodes on the
boundary of the convex hull, which
facilitates imposition of essential boundary conditions. A
methodology to model material
discontinuities and non-convex bodies (cracks) using
NEM is also described. A standard
displacement-based Galerkin procedure is used to obtain the
discrete system of linear equations. Application
of NEM to various problems in solid mechanics, which include,
the patch test, gradient problems, bimaterial interface,
and a static crack problem are presented. Excellent agreement with
exact (analytical) solutions is obtained, which exemplifies the
accuracy and robustness of NEM and suggests its potential
application in the context of other classes of problems--crack
growth, plates, and large deformations to name a few.
This paper is available in gzipped postscript
format (71 pages, ~1.6MB gzipped) as well as in
PDF.
C1 Natural Neighbor
Interpolant for Partial Differential Equations
N. Sukumar and B. Moran
Numerical Methods for Partial Differential Equations
Vol. 15, Number 4, pp. 417-447, 1999
Abstract
Natural neighbor coordinates
(Sibson, 1980)
are
optimum weighted-average measures for an irregular
arrangement of nodes in Rn.
Farin (1990)
used the notion of Bezier
simplices in natural neighbor coordinates
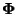 to propose a C1
interpolant. The
C1 interpolant has quadratic
precision in
to propose a C1
interpolant. The
C1 interpolant has quadratic
precision in
 , and
reduces to a cubic polynomial between
adjacent nodes on
the boundary , and
reduces to a cubic polynomial between
adjacent nodes on
the boundary
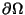 . We
present the
C1 formulation and
propose a computational methodology for its
numerical implementation (Natural Element
Method) for the solution of partial differential
equations (PDEs). The
approach involves the
transformation of the original Bernstein basis functions . We
present the
C1 formulation and
propose a computational methodology for its
numerical implementation (Natural Element
Method) for the solution of partial differential
equations (PDEs). The
approach involves the
transformation of the original Bernstein basis functions
 to new shape functions
to new shape functions
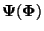 ,
such that the shape functions ,
such that the shape functions
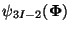 , ,
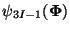 , and , and
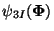 for
node I are directly associated with the three nodal degrees
of freedom for
node I are directly associated with the three nodal degrees
of freedom
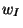 , ,
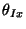 , and , and
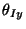 ,
respectively. The
C1 shape functions interpolate to nodal function
and nodal gradient values, which renders the interpolant
amenable to application in a Galerkin scheme for the
solution of fourth-order elliptic PDEs. Results for the
biharmonic equation with Dirichlet boundary conditions are
presented. The generalized eigenproblem is studied to
establish the ellipticity of the discrete biharmonic operator,
and consequently the stability of the numerical method. ,
respectively. The
C1 shape functions interpolate to nodal function
and nodal gradient values, which renders the interpolant
amenable to application in a Galerkin scheme for the
solution of fourth-order elliptic PDEs. Results for the
biharmonic equation with Dirichlet boundary conditions are
presented. The generalized eigenproblem is studied to
establish the ellipticity of the discrete biharmonic operator,
and consequently the stability of the numerical method.
This paper is available in gzipped postscript
format (56 pages, ~1.2MB gzipped) as well as in
PDF.
Dispersive Properties of the Natural
Element Method
D. Bueche, N. Sukumar and B. Moran
Computational Mechanics
Vol. 25, Number 2/3, pp. 207-219, 2000
Abstract
The Natural Element Method (NEM) is a mesh-free numerical method for
the solution of partial differential equations. In the natural
element method, natural neighbor coordinates, which are
based on the Voronoi tesselation of a set of nodes, are used to
construct the interpolant. The performance of NEM in two-dimensional
linear elastodynamics is investigated. A standard Galerkin formulation
is used to obtain the weak form and a central-difference time
integration scheme is chosen for time history analyses. Two different
applications are considered: vibration of a cantilever beam and
dispersion analysis of the wave equations. The NEM results are compared
to finite element and analytical solutions. Excellent dispersive
properties of NEM are observed and good agreement with analytical
solutions is obtained.
This paper is available in gzipped postscript
format (28 pages, ~0.8MB gzipped) as well as in
PDF.
Natural Neighbor Galerkin Methods
N. Sukumar, B. Moran, A. Yu Semenov and V. V. Belikov
International Journal for Numerical Methods in Engineering
Vol. 50, Number 1, pp. 1-27, 2001
Abstract
Natural neighbor coordinates (Sibson coordinates) is a well-known
interpolation scheme for multivariate data fitting and smoothing.
The numerical implementation of natural neighbor coordinates in a
Galerkin method is known as the Natural Element Method (NEM). In the
natural element method, natural neighbor coordinates are
used to construct the trial and test functions. Recent studies
on NEM (Sukumar et al. (1998),
Sukumar and Moran (1999))
have shown that natural neighbor
coordinates, which are based on the Voronoi tessellation of a set of nodes,
are an appealing choice
to construct meshless interpolants for the solution of partial
differential equations. In Belikov et al. (1997),
a new interpolation
scheme (non-Sibsonian interpolation) based on natural neighbors was
proposed. In the present paper, the non-Sibsonian interpolation scheme is
reviewed and its performance in a Galerkin method for the solution of
elliptic partial differential equations that arise in linear
elasticity is studied. A methodology to
couple finite elements to NEM is also described.
Two significant advantages of the non-Sibson interpolant over the Sibson
interpolant are revealed and numerically verified: the computational
efficiency of the non-Sibson algorithm in 2-dimensions, which is
expected to carry over to 3-dimensions, and the ability to exactly impose
essential boundary conditions on the boundaries of convex and
non-convex domains.
This paper is available in gzipped postscript
format (43 pages, ~1.1MB gzipped) as well as in
PDF (27 pages, ~0.3MB)
Voronoi Cell Finite Difference Method for the Diffusion
Operator on Arbitrary Unstructured Grids
N. Sukumar
International Journal for Numerical Methods in Engineering
Vol. 57, Number 1, pp. 1-34, 2003
Abstract
Voronoi cells and the notion of natural neighbors are used to develop a
finite difference method for the diffusion operator
on arbitrary unstructured grids. Natural neighbors are
based on the Voronoi diagram, which partitions space into
closest-point regions.
The Sibson and the Laplace (non-Sibsonian)
interpolants which are based on natural neighbors
have shown promise within a Galerkin framework for
the solution of partial differential equations.
In this paper, we focus on the Laplace interpolant
with a two-fold objective: first, to unify the
previous developments related to the Laplace interpolant and
to indicate its ties to some well-known numerical methods;
and secondly to propose a Voronoi cell
finite difference scheme for the
diffusion operator on arbitrary unstructured grids.
A conservation law in integral
form is discretized on Voronoi cells to derive a
finite difference scheme for the diffusion operator on irregular
grids. The proposed scheme can also be viewed as a point
collocation technique. A detailed study on consistency is
conducted, and the satisfaction of
the discrete maximum principle (stability) is established.
Owing to symmetry of the Laplace weight, a symmetric positive-definite
stiffness matrix is realized which permits the use of efficient
linear solvers. On a regular (rectangular or hexagonal) grid, the
difference scheme reduces to
the classical finite difference method. Numerical
examples for the Poisson equation with Dirichlet boundary conditions
are presented to demonstrate the accuracy and convergence of the
finite difference scheme.
This paper is available in PDF (34 pages,
~7.4MB).
|

