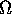
We assume the discrete model of a body 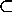R² consists of a set of distinct nodes N, and a polygonal description of the boundary . In the natural element method, the trial and test functions are constructed using natural neighbor interpolants. These interpolants are based on the Voronoi tessellation of the set of nodes N. The NEM interpolant is strictly linear between adjacent nodes on the boundary of the convex hull, which facilitates imposition of essential boundary conditions. A methodology to model material discontinuities and non-convex bodies such as cracks is described. A standard displacement-based Galerkin procedure is used to obtain the discrete system of linear equations. Application of NEM to various problems in two-dimensional elastostatics is presented.

The construction and computational implementation of a C¹ natural neighbor interpolant for fourth-order elliptic PDEs is presented. By embedding natural neighbor interpolants in the surface representation of a Bernstein-Bezier cubic simplex, a C¹ interpolant is realized (Farin, 1990). We present the C¹ formulation and propose a computational methodology for its numerical implementation for the solution of PDEs. Numerical results for the biharmonic equation with Dirichlet boundary conditions are presented.

A mixed formulation for the natural element method in linear elastostatics is presented. A displacement-pressure mixed formulation is adopted with displacements interpolated by C⁰ natural neighbor interpolants; C⁰ and C^-1 interpolation schemes are considered for the interpolation of the pressure. The mixed C⁰-C^-1 NEM formulation alleviates locking in the near incompressible limit for the elastostatic boundary value problem; moreover, convergence rates in displacement and energy are optimal for all 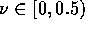. Results for benchmark problems in compressible and incompressible elasticity are presented.

The entire thesis is available in gzipped postscript format, PDF, or individual chapters of the thesis can be downloaded. The EPS figures in the thesis are available as a gzipped tar archive.

Slides presented at the Ph.D. defense on May 8, 1998 [Landscape] [Portrait]

Ph.D. Thesis (Ph.D. Thesis, Gzipped PS, 217 pages, 2.8MB)

1. Preliminary Pages [Title, Abstract, Acknowledgements, TOC, etc.] [PS, 11 pages, 130K]
2. Chapter 1 [Introduction] [PS, 8 pages, 82K]
3. Chapter 2 [Galerkin Method for Linear Elliptic Problems] [PS, 15 pages, 158K]
4. Chapter 3 [Natural Neighbor Interpolation] [PS, 48 pages, 7.0MB]
5. Chapter 4 [Natural Element Method for Two-Dimensional Elasticity] [PS, 49 pages, 645K]
6. Chapter 5 [C¹ Natural Neighbor Interpolant for the Biharmonic Equation] [PS, 49 pages, 5.7MB]
7. Chapter 6 [Mixed Natural Element Method in Linear Elasticity] [PS, 21 pages, 247K]
8. Chapter 7 [Conclusions] [PS, 5 pages, 50K]
9. References [References] [PS, 11 pages, 84K]
10. Errata [Errata] [PS, 1 page, 21K]

Downloading Instructions

• NEM 2D Code [Gzipped tar file, 1.3MB] [Zip archive, 1.3MB]

Please read the README file (ASCII), which is also included in the NEM distribution, for further details about the NEM program.

Comments/Questions