Quadratic Precision

Farin [1] has outlined many properties of the $C^1(\Omega)$ interpolant given in Eq. (8). Here we discuss some of the important properties that are germane to a displacement-based Galerkin formulation that is pursued in this paper.

The $C^1(\Omega)$ interpolant has quadratic precison [1], i.e. it can exactly reproduce a quadratic displacement field. As opposed to the above, the $C^1(\Omega)$ interpolant proposed by [15] can only reproduce spherical quadratics, i.e. functions of the form $\alpha(x^2 - y^2)$. By virtue of the quadratic precision property, the $C^1(\Omega)$ NEM interpolant can exactly represent a state of constant curvature (second-derivatives of displacement) which is required in order to pass the patch test for a fourth-order PDE such as the biharmonic equation.

By judicious choice of the Bézier ordinates, [16] realized a quadratic precision interpolant. For a cubic $n$-gon simplex, there are $n^2 + \binom{n}{3}$ control points, and consequently the same number of Bézier ordinates. Of these, $n^2$ control points lie along the line joining vertices $\mathbf{q}_{ {\mathbf{i}}}$ and $\mathbf{q}_{ {\mathbf{j}}}$. The associated ``boundary'' Bézier ordinates to these $n^2$ control points have either one 3 and all other zeros (e.g. $b_{0,3,0,0}$ for $n=4$) or one 2, one 1, and other zeros (e.g. $b_{1,2,0,0}$ for $n=4$). The former (vertex or corner ordinates) are equal to the nodal function value, while the latter Bézier ordinates are easily found in the tangent planes. The additional $\binom{n}{3}$ ``free'' parameters are those which have three 1's and all other zeros (e.g. $b_{1,1,1,0}$ for $n=4$). An optimal choice for the center Bézier ordinate is given by $b_{1,1,1,0} = \frac{3}{2}a - \frac{1}{2}c$ [16], where $a$ is the centroid of the tangent Bézier ordinates while $c$ is the centroid of the vertex (corner) Bézier ordinates. The above choice of the center Bézier ordinate guarantees quadratic precision. An illustration of the calculation of the Bézier ordinates for a cubic triangular patch is shown in Fig. 2.1. Referring to Fig. 2.1, we can express $b_{1,1,1}$ as

$$b_{1,1,1,0} = \frac{3}{2}a - \frac{1}{2}c ,$$ (9)

where

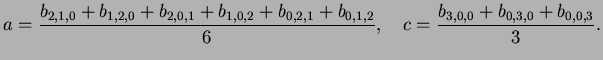$$a = \frac{b_{2,1,0} + b_{1,2,0} + b_{2,0,1} + b_{1,0,2} + b_{0,2,1} + b_{0,1,2}}{6} , \quad c = \frac{b_{3,0,0} + b_{0,3,0} + b_{0,0,3}}{3}.$$ (10)