


Next: NEM Interpolant
Up: A NEM Interpolant for
Previous: A NEM Interpolant for
The ability to develop
 interpolants
over an arbitrary bounded domain
interpolants
over an arbitrary bounded domain 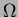 is a much researched
and far from trivial task. In the realm of finite elements, one
of the first
is a much researched
and far from trivial task. In the realm of finite elements, one
of the first
 interpolants developed was the
Clough-Tocher finite element [3], and in
subsequent years many of its variants have emerged
[4,5,6,7].
The higher-order smoothness or continuity requirement of interpolants
is of interest since such class of trial
functions are stipulated in a Galerkin forumulation
for the solution of higher-order elliptic partial differential
equations--
interpolants developed was the
Clough-Tocher finite element [3], and in
subsequent years many of its variants have emerged
[4,5,6,7].
The higher-order smoothness or continuity requirement of interpolants
is of interest since such class of trial
functions are stipulated in a Galerkin forumulation
for the solution of higher-order elliptic partial differential
equations--
 trial functions for the
biharmonic (fourth-order)
equation in elasticity, with particular emphasis on
thin plate Kirchhoff bending being a notable application
and a case in point.
trial functions for the
biharmonic (fourth-order)
equation in elasticity, with particular emphasis on
thin plate Kirchhoff bending being a notable application
and a case in point.
In the interest of brevity, we
directly proceed to present Farin's
 formulation, without
touching upon the foundations of Sibson's
original natural neighbor interpolant [2].
For some familiarity with the Sibson
interpolant and its application to
second-order partial differential equations in
mechanics, the interested reader can
refer to [8] and [9],
and the references therein.
formulation, without
touching upon the foundations of Sibson's
original natural neighbor interpolant [2].
For some familiarity with the Sibson
interpolant and its application to
second-order partial differential equations in
mechanics, the interested reader can
refer to [8] and [9],
and the references therein.
N. Sukumar
![]() formulation, without
touching upon the foundations of Sibson's
original natural neighbor interpolant [2].
For some familiarity with the Sibson
interpolant and its application to
second-order partial differential equations in
mechanics, the interested reader can
refer to [8] and [9],
and the references therein.
formulation, without
touching upon the foundations of Sibson's
original natural neighbor interpolant [2].
For some familiarity with the Sibson
interpolant and its application to
second-order partial differential equations in
mechanics, the interested reader can
refer to [8] and [9],
and the references therein.