Numerical Implementation
On considering the dual formulation, the solution for
the Lagrange multipliers can be written as [16,17]
 |
(5) |
where
 is the optimal solution that is desired.
Since
is the optimal solution that is desired.
Since 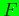 is strictly convex in the interior of
is strictly convex in the interior of  ,
convex optimization algorithms (for example, Newton's method and
families of gradient descent) are a natural choice. The steps
in these algorithm are:
,
convex optimization algorithms (for example, Newton's method and
families of gradient descent) are a natural choice. The steps
in these algorithm are:
- Start with iteration counter
 . The initial guess
. The initial guess
 and let
and let  be the desired
convergence tolerance. For the convergence tolerance,
be the desired
convergence tolerance. For the convergence tolerance,
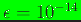 -
- is
suitable (see sample input data files in the tests
sub-directory);
is
suitable (see sample input data files in the tests
sub-directory);
- Compute
 (gradient of
(gradient of 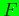 ) and
) and
 (Hessian of
(Hessian of 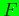 );
);
- Determine a suitable search direction,
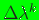 .
For steepest descent,
.
For steepest descent,
 and for Newton's method,
and for Newton's method,
 (matrix-vector notation) are used;
(matrix-vector notation) are used;
- Update:
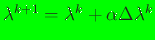 , where
, where 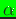 is the step size.
For steepest descent, a variable step size (line
search) algorithm, which is presented in Reference [18],
is used to determine
is the step size.
For steepest descent, a variable step size (line
search) algorithm, which is presented in Reference [18],
is used to determine
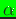 , and for Newton's method (damped or guarded),
the line search is used to set the step size if the error is
greater than
, and for Newton's method (damped or guarded),
the line search is used to set the step size if the error is
greater than 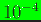 and otherwise,
and otherwise,
 is used;
is used;
- Check convergence: if
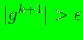 , increment
the iteration
counter,
, increment
the iteration
counter,
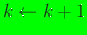 , and goto 2, else continue;
, and goto 2, else continue;
- Set
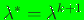 and
compute the max-ent basis functions using Eq. (4).
and
compute the max-ent basis functions using Eq. (4).
N. Sukumar
Copyright © 2008