Shannon [1] introduced the concept of entropy in
information theory, with an eye on its applications in
communication theory.
The general form of informational entropy (Shannon-Jaynes or relative
entropy functional) is [2,3,4]:
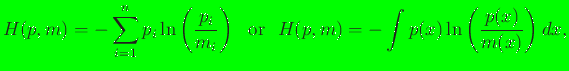 |
(1) |
where  is a
is a  -estimate (prior distribution).
The quantity
-estimate (prior distribution).
The quantity
 is also referred to as the Kullback-Leibler (KL) distance. As a means
for least-biased statistical
inference in the presence of testable constraints, Jaynes's used the
Shannon entropy to propose the principle of maximum entropy [5],
and if the KL-distance is adopted as the objective functional,
the variational principle is known as the principle of minimum relative
entropy [4].
is also referred to as the Kullback-Leibler (KL) distance. As a means
for least-biased statistical
inference in the presence of testable constraints, Jaynes's used the
Shannon entropy to propose the principle of maximum entropy [5],
and if the KL-distance is adopted as the objective functional,
the variational principle is known as the principle of minimum relative
entropy [4].
Consider a set of distinct nodes in
 that are located at
that are located at
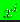 (
(
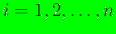 ),
with
),
with
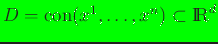 denoting the
convex hull of the nodal set. For a
real-valued function
denoting the
convex hull of the nodal set. For a
real-valued function
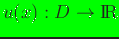 , the
numerical approximation for
, the
numerical approximation for  is:
is:
 |
(2) |
where 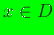 ,
,
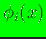 is the basis function associated
with node
is the basis function associated
with node 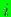 , and
, and 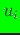 are coefficients. The use of basis
functions that are constructed independent of an underlying
mesh has become popular in the past decade--meshfree Galerkin
methods are a common target application for such approximation
schemes [6,7,8,9,10].
The construction of basis functions using information-theoretic
variational principles is a new development
[11,12,13,14];
see Reference [14] for a recent review
on meshfree basis functions. To obtain basis functions using the
maximum-entropy formalism, the Shannon entropy functional
(uniform prior) and a modified
entropy functional (Gaussian prior) were introduced in
References [11] and [12], respectively,
which was later generalized by adopting the Shannon-Jaynes
entropy functional (any prior) [14].
The implementation of these new basis functions has been carried
out, and this manual describes a Fortran 90 library for
computing maximum-entropy (max-ent) basis functions and their first
and second derivatives for any prior weight function.
are coefficients. The use of basis
functions that are constructed independent of an underlying
mesh has become popular in the past decade--meshfree Galerkin
methods are a common target application for such approximation
schemes [6,7,8,9,10].
The construction of basis functions using information-theoretic
variational principles is a new development
[11,12,13,14];
see Reference [14] for a recent review
on meshfree basis functions. To obtain basis functions using the
maximum-entropy formalism, the Shannon entropy functional
(uniform prior) and a modified
entropy functional (Gaussian prior) were introduced in
References [11] and [12], respectively,
which was later generalized by adopting the Shannon-Jaynes
entropy functional (any prior) [14].
The implementation of these new basis functions has been carried
out, and this manual describes a Fortran 90 library for
computing maximum-entropy (max-ent) basis functions and their first
and second derivatives for any prior weight function.
We use the relative entropy functional given in Eq. (1)
to construct max-ent basis functions.
The variational formulation for maximum-entropy approximants is:
find
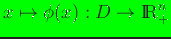 as the
solution of the following constrained (convex or concave with
as the
solution of the following constrained (convex or concave with  or
or  , respectively) optimization problem:
, respectively) optimization problem:
where
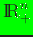 is the non-negative orthant,
is the non-negative orthant,
 is a non-negative weight function (prior
estimate to
is a non-negative weight function (prior
estimate to  ), and
the linear constraints form an under-determined system.
On using the method of Lagrange multipliers,
the solution of the variational problem is [14]:
), and
the linear constraints form an under-determined system.
On using the method of Lagrange multipliers,
the solution of the variational problem is [14]:
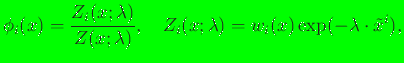 |
(4) |
where
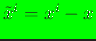 (
(
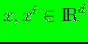 )
are shifted nodal coordinates,
)
are shifted nodal coordinates,
 are the
are the  Lagrange multipliers
(implicitly dependent on the point
Lagrange multipliers
(implicitly dependent on the point 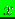 )
associated with the constraints in Eq. (3c),
and
)
associated with the constraints in Eq. (3c),
and
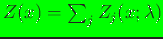 is known as the partition function
in statistical mechanics. The smoothness of maximum-entropy basis functions
for the Gaussian prior was established
in Reference [12]; the continuity for any
is known as the partition function
in statistical mechanics. The smoothness of maximum-entropy basis functions
for the Gaussian prior was established
in Reference [12]; the continuity for any 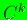 (
( )
prior was proved in Reference [15].
)
prior was proved in Reference [15].
N. Sukumar
Copyright © 2008
![]() that are located at
that are located at
![]() (
(
![]() ),
with
),
with
![]() denoting the
convex hull of the nodal set. For a
real-valued function
denoting the
convex hull of the nodal set. For a
real-valued function
![]() , the
numerical approximation for
, the
numerical approximation for ![]() is:
is:
![]() as the
solution of the following constrained (convex or concave with
as the
solution of the following constrained (convex or concave with ![]() or
or ![]() , respectively) optimization problem:
, respectively) optimization problem: