In priorweightfunction.f90, all subroutines and functions are
contained within the priorweightfunction module. The
radius of support for the nodal weight functions, metric D, and
the prior are set in
subroutine setrmaxandpriorweight( ). This is done
via a call to this function from an external program or from
subroutine drivermaxent(
). This is done
via a call to this function from an external program or from
subroutine drivermaxent( ), which
is contained in the maxent module. The main program,
main.f90, serves as an illustrative reference.
The variables rmax, D, and prior are
private variables,
and hence once they are set, all
functions within the module can access them.
The weight functions are defined in
function weightfunction(
), which
is contained in the maxent module. The main program,
main.f90, serves as an illustrative reference.
The variables rmax, D, and prior are
private variables,
and hence once they are set, all
functions within the module can access them.
The weight functions are defined in
function weightfunction(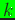 ,
,
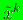 ,
,
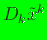 ,
,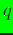 ).
Here,
).
Here, 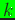 runs from
runs from  to
to 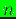 ,
,
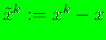 , and
, and
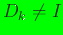 renders the nodal weight function support to be anisotropic.
The variable
renders the nodal weight function support to be anisotropic.
The variable
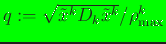 ,
where
,
where
 is the radius of support of the nodal
weight function. The following weight functions are available:
is the radius of support of the nodal
weight function. The following weight functions are available:
- uniform: a constant weight function, i.e.,
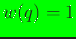 .
.
- cubic: the weight function is a
 cubic
spline function, which is given by
cubic
spline function, which is given by
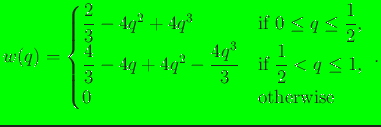 |
(19) |
- quartic: the weight function is a
 quartic
polynomial function, which is given by
quartic
polynomial function, which is given by
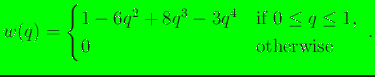 |
(20) |
- gaussian: the weight function is a
 Gaussian
function, which is given by
Gaussian
function, which is given by
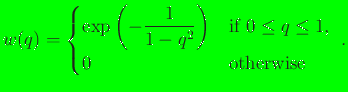 |
(21) |
- gaussian-rbf: a
 Gaussian radial basis function,
Gaussian radial basis function,
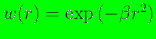 [12],
where
[12],
where
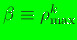 is a constant
for each node.
is a constant
for each node.
If a different prior is desired, it can be added in
function weightfunction( ).
The gradient is defined in
function dweightfunction(
).
The gradient is defined in
function dweightfunction( ), and
the Hessian of the weight function is defined in
function ddweightfunction(
), and
the Hessian of the weight function is defined in
function ddweightfunction( ).
).
N. Sukumar
Copyright © 2008