


Next: Natural Neighbor Interpolation
Up: A Note on Natural
Previous: Introduction
The Voronoi diagram and its dual, Delaunay tessellation
(covering of a surface with tiles) are geometric
constructs that are widely used in the field of
computational geometry. For simplicity, and for the
purpose of illustration, we consider
two-dimensional Euclidean space
 ; the
theory, however, is applicable in a general
; the
theory, however, is applicable in a general  -dimensional
framework. Consider a set of distinct points (nodes)
-dimensional
framework. Consider a set of distinct points (nodes)
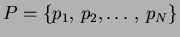 in
in
 . The
tile (also known as Thiessen or Voronoi polygon) of
. The
tile (also known as Thiessen or Voronoi polygon) of
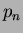 is defined as [1]
is defined as [1]
 |
(1) |
where
 is the Euclidean metric.
Each tile
is the Euclidean metric.
Each tile 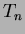 is the intersection of finitely many open
half-spaces, each being delimited by the perpendicular
bisector (hyperlane in
is the intersection of finitely many open
half-spaces, each being delimited by the perpendicular
bisector (hyperlane in
 ). In simpler terms,
the tile
). In simpler terms,
the tile 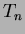 can be viewed as the locus of all points closer to
can be viewed as the locus of all points closer to
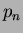 than to any other node. If
than to any other node. If  , it is
readily seen that the locus is the perpendicular bisector
of the line joining the nodes, while if
, it is
readily seen that the locus is the perpendicular bisector
of the line joining the nodes, while if  ,
the perpendicular bisector of the sides of the triangle
(
,
the perpendicular bisector of the sides of the triangle
(
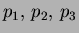 ) which meet at the circumcenter of the triangle
defines the Voronoi diagram. Generalizing, we see that
the Voronoi diagram for a set of nodes divides the plane
into a set of regions, one for each node, such that any point in
a particular region is closer to that region's node than to any other
node. The Delaunay triangles are constructed by connecting
the nodes whose Voronoi cells have common boundaries. The
Delaunay triangulation and the Voronoi diagram are
dual structures -- each contains the same ``information''
in some sense, but represented in a different form. See
[11] and [12] for details on Voronoi
polygons. A nice exposition and comprehensive survey on
Voronoi diagrams can be found in [13].
) which meet at the circumcenter of the triangle
defines the Voronoi diagram. Generalizing, we see that
the Voronoi diagram for a set of nodes divides the plane
into a set of regions, one for each node, such that any point in
a particular region is closer to that region's node than to any other
node. The Delaunay triangles are constructed by connecting
the nodes whose Voronoi cells have common boundaries. The
Delaunay triangulation and the Voronoi diagram are
dual structures -- each contains the same ``information''
in some sense, but represented in a different form. See
[11] and [12] for details on Voronoi
polygons. A nice exposition and comprehensive survey on
Voronoi diagrams can be found in [13].



Next: Natural Neighbor Interpolation
Up: A Note on Natural
Previous: Introduction
N. Sukumar