If one wants to use the max-ent library with any other program, then
first create the static library file libmaxent.a by
invoking make maxentlib in the top-directory.
Let the environment variable MAXENTDIR
point to where MAXENT-V1.4 is located. The library file is
at $(MAXENTDIR)/MAXENT-V1.4/lib/libmaxent.a. To link
this library file with any other Fortran 90 program, the following
command can be used:
g95 -o a.out <object-files> -L $(MAXENTDIR)/MAXENT-V1.4/lib -lmaxent
If an interface from a C or C ++ program is required, the appropriate
call (depending on the compiler and the operating system) should be invoked.
The subroutine call from a Fortran 90 program to compute the max-ent basis
functions is given below (see main.f90 and also maxent.f90 for
further details):
call drivermaxent(n,nsd,scheme,prior,xyz,p,rmax,D,maxit,eps,printflag,errorflag,lengthscale,dettol,phi,dphi,ddphi)
The input parameters in the above subroutine are as follows:
- n : number of neighbors of point
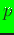 (a positive integer);
(a positive integer);
- nsd : spatial dimension (a positive integer);
- scheme : either descent, newton, or
lbfgs (a string);
- prior : either uniform, cubic, quartic,
gaussian, or gaussian-rbf (a string);
- xyz : nodal coordinates of the
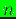 neighbors (double
precision array xyz(n,nsd));
neighbors (double
precision array xyz(n,nsd));
- p : coordinates of the point
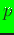 (double precision array
p(nsd));
(double precision array
p(nsd));
- rmax : support sizes of the
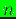 neighbors (double precision
array rmax(n));
neighbors (double precision
array rmax(n));
- D : anisotropic metric (double precision array D(nsd,nsd,n));
- maxit : maximum number of iteration (a positive integer);
- eps : convergence tolerance (double precision);
- printflag : print convergence information
(logical: .true. or .false.);
- errorflag : error flag (
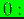 pass,
pass, 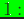 Hessian too small;
Hessian too small; 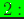 non-convergence in maxit iterations);
non-convergence in maxit iterations);
- lengthscale : length scale for domain (optional argument) so that convergence criterion is independent of the magnitude of nodal coordinates;
- dettol : determinant tolerance (optional argument) with default of

The output variables (phi, dphi, and ddphi)
in the parameter-list are defined as optional:
- phi : basis function vector (double precision
phi(n));
- dphi : 1st derivatives of basis functions (double precision
dphi(nsd,n));
- ddphi : 2nd derivatives of basis functions (double precision
ddphi(nsd*nsd,n));
Please note that any calling subroutine must first
determine for every
point 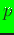 , the
number of neighbors
, the
number of neighbors 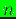 for
for 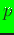 , assign
the nodal coordinates of these
, assign
the nodal coordinates of these 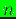 nodes to the array xyz,
and the support sizes of these
nodes to the array xyz,
and the support sizes of these 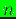 nodes must be assigned to
the array rmax.
Then only can a call to the subroutine
drivermaxent
nodes must be assigned to
the array rmax.
Then only can a call to the subroutine
drivermaxent be invoked.
It is assumed that computations for dphi and/or
ddphi are requested in conjunction with phi. Hence,
in the parameter-list,
phi (
be invoked.
It is assumed that computations for dphi and/or
ddphi are requested in conjunction with phi. Hence,
in the parameter-list,
phi ( is computed), phi and dphi
(
is computed), phi and dphi
( and
and
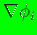 are computed),
phi and ddphi (
are computed),
phi and ddphi ( and
and
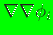 are computed), or all three
(
are computed), or all three
( ,
,
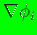 and
and
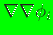 are computed) are valid.
are computed) are valid.
N. Sukumar
Copyright © 2008