


Next: Acknowledgements
Up: A Note on Natural
Previous: A Study in Contrast:
In the preceding sections, a concise description of
natural neighbor interpolation and its implementation in
the context of a Galerkin procedure to solve PDEs was
delineated. Having at least given a flavor (I hope) of
the interpolation scheme, one can be undoubtedly ambitious
in suggesting its possible applications within the field
of computational mechanics:
- Patch test: The first step in the testing of a numerical
method for the elliptic operator. The patch test is a
sufficient condition to prove the convergence of
a numerical method [22].
- Smooth boundary-value problems in elastostatics (2D) -- plate
with a circular/elliptical hole, beam in bending, etc.
- Benchmark crack problems in 2D: The edge-crack, center-crack,
and shear crack problems, where symmetric boundary conditions
can be imposed. The case of inclined
cracks (no planes of symmetry) might pose a problem, since the
whole domain has to be modeled -- non-convex domain!
- The higher order smoothness (or regularity) of the
NEM interpolant in
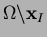 allows
one to consider higher order PDEs [10]. The
FE interpolant,
allows
one to consider higher order PDEs [10]. The
FE interpolant,
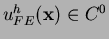 , since
, since
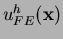 is continuous but its gradients are
discontinuous across element
boundaries (edges of the Delaunay triangle). The
approach used
by [23] to successfully avoid
locking in beams and plates by using cardinal splines on
regular grids can be explored using NEM in the context
of irregular nodal arrangements. The jumps in the displacement
gradients at the nodes do not pose a problem since the
numerical integration is carried out inside the triangle.
is continuous but its gradients are
discontinuous across element
boundaries (edges of the Delaunay triangle). The
approach used
by [23] to successfully avoid
locking in beams and plates by using cardinal splines on
regular grids can be explored using NEM in the context
of irregular nodal arrangements. The jumps in the displacement
gradients at the nodes do not pose a problem since the
numerical integration is carried out inside the triangle.
- Finite deformation: Mesh distortion and
mesh entanglement which are the bane of FE are not issues in
NEM. The density of the nodes dictates the quality of the
n-n interpolation and not the Delaunay triangles.
- Fluid-structure interaction: See [10].
- Moving interfaces




Next: Acknowledgements
Up: A Note on Natural
Previous: A Study in Contrast:
N. Sukumar