Instructions -- 3D Elements

The plotter applet for 3D elements is conceptually very similar to the applet for 2D elements.






The first step is to form a polyhedral element. Nothing else can be done until this step has been taken. This is done by entering the number of nodes as shown. We will use the minumum of 4. The polyhedron is formed by placing the nodes at random and then arranging them in such a way that they are as far from each other as possible on the unit sphere. This results in a convex polyhedron.






Our four nodes have been placed to form a tetrahedron. The "Rand" button would place a given number of nodes at random inside the polyhedron.






Plotting in the 3D applet is performed by taking the intersection of a plane with the solid polyhedron. When plotting is first enabled, the intersecting plane is the x-y plane. So what we see above is the shape function for the first node on the x-y plane.






The intersecting plane is repositioned by rotating the view and then clicking the right mouse button. The plane is then positioned such that it passed through the origin and its normal points toward the viewer.






The plane can also be slid along its normal by moving the mousewheel. Here it is moved out toward the face of the tetrahedron, axes are turned off, and plotting quality is turned up. The quality should be turned down while moving the intersecting plane, since this process is computationally expensive.





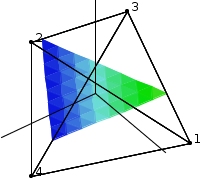
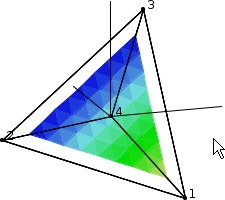
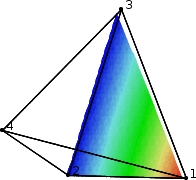
The rest of the controls are similar to the 2D applet's. New nodes may only be input on the inside of the polyhedron. Also, only interior nodes may be removed individually. As of this writing, the only formulation available is Maximum Entropy. And of course, values may be calculated anywhere inside the polyhedron.




Last update: 6/20/2006
This work is supported by the National Science Foundation under Grant #DMS-0135345.