


Next: Applications in Computational Mechanics
Up: A Note on Natural
Previous: Implementation of the Natural
A comparison of FEM, EFG, and NEM follows:
- The interpolant in both FEM and NEM possess similar
properties (see Section 3), and the interpolants
are exactly the same in 1D. The EFG trial function
does possess linear consistency but is not an
interpolant; hence, Lagrange multipliers or a coupling
with FE is required to satisfy the essential boundary
conditions.
- A ``similar'' (in principle) mesh structure (triangulation)
is used in both FE and NEM, while the approximant in
EFG (a ``meshless method'') is constructed solely on the
basis of a set of nodes and a weight function with compact
support.
- In all three methods, the interpolant/approximant has a
local character because of the compact support of the
shape functions
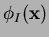 .
.
- In FE, the functional that is integrated over the domain
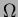 in the weak form is constructed using a polynomial
trial function and hence we can obtain an accurate
estimate of the integral using Gauss-Legendre quadrature
(within machine precision and round-off errors). As opposed
to FE, in both NEM and EFG (moreso probably in EFG), the
shape functions are not polynomials in general. Hence
numerical integration is
an issue and the question of optimum/accurate quadrature
arises, which is still an open issue. In [10],
three-point Gauss-Legendre quadrature was found to be
sufficient to obtain accurate results.
in the weak form is constructed using a polynomial
trial function and hence we can obtain an accurate
estimate of the integral using Gauss-Legendre quadrature
(within machine precision and round-off errors). As opposed
to FE, in both NEM and EFG (moreso probably in EFG), the
shape functions are not polynomials in general. Hence
numerical integration is
an issue and the question of optimum/accurate quadrature
arises, which is still an open issue. In [10],
three-point Gauss-Legendre quadrature was found to be
sufficient to obtain accurate results.
- In the discrete system
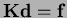 , the stiffness
matrix
, the stiffness
matrix
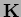 is banded in FEM, while in both EFG and NEM,
is banded in FEM, while in both EFG and NEM,
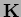 is not banded in general.
is not banded in general.
- The computational cost (apart from numerical issues) is
an important factor in the feasibility and usability of a
numerical method. Finite elements, apart from their nice
local (polynomial) properties, are a computationally
attractive choice because of the very fast execution
times that are attainable. The key time-consuming steps
in the NEM are:
- Dirichlet tessellation (Voronoi diagram) of the
nodes -- for some typical algorithms, see
[17,18,19].
In 2D, Fortune's `sweepline' algorithm
[18] is considered to be one of the fastest,
while in higher dimensions, the Qhull package
[20] based on the `quickhull' algorithm
[19] appears to be the unanimous choice.
Both the above are
 algorithms.
algorithms.
- Search for natural neighbors for a sampling point
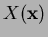 . The walking-triangle algorithm due to
Lawson [21], which is a
. The walking-triangle algorithm due to
Lawson [21], which is a
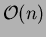 algorithm, is a suitable choice.
algorithm, is a suitable choice.
[10] used the Qhull package [20]
for the Dirichlet tessellation and Lawson's algorithm
[21] for the neighbor-search. They
have reported [10] execution times for NEM that
are about a factor of two slower than quadratic finite elements.



Next: Applications in Computational Mechanics
Up: A Note on Natural
Previous: Implementation of the Natural
N. Sukumar
 algorithms.
algorithms.
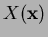 . The walking-triangle algorithm due to
Lawson [21], which is a
. The walking-triangle algorithm due to
Lawson [21], which is a
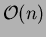 algorithm, is a suitable choice.
algorithm, is a suitable choice.